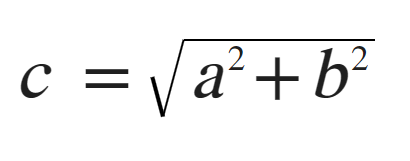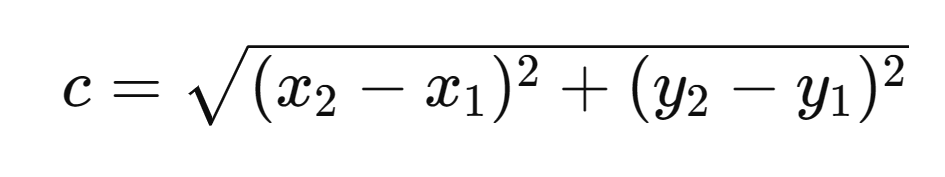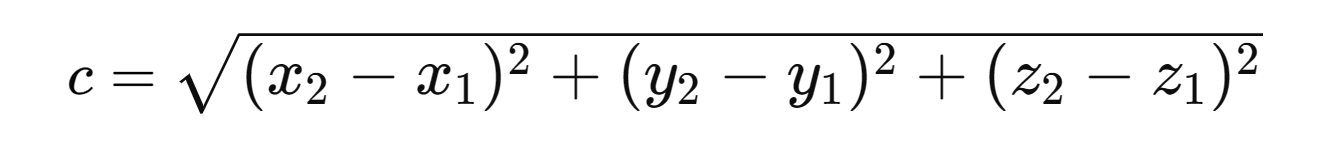How To Calculate Distance In Nuke
This is a little trick I’ve used in the past to animate values like Depth of Field, or 2D screen space effects, like blurs, erodes, and glows. It is slightly different from using a standard depth pass because it works for animated elements that change distance frequently. Using it as an expression also allows for live results.
Understanding the Math
Before we jump into making this in Nuke, let’s take a moment to understand what is going on. It’s not complicated, I promise! Do you remember that guy named Pythagoras? No? That’s alright, I honestly forgot about him too, until I needed this calculation. Turns out Pythagoras came up with a simple way to calculate the distance between two points, and we can use this ancient knowledge in Nuke.
Let’s start with a simple 2D example first. Imagine two 2D points in your viewer, with coordinates (x₁, y₁) and (x₂, y₂)
You might be thinking “The Pythagorean theorem is for calculating the hypotenuse of a right angle triangle. How does that help us find the distance between anything?” Well… you are smarter than I thought, but let’s take another look at those points, shall we?
How about that? A right angle triangle was hidden there all along! One of the joys of learning math, is you start to see secret things everywhere. Now, since finding the hypotenuse is solving for the length of C, it is also the same thing as finding the distance between our two points. Below is the Pythagorean Theorem, but it requires us to know the length of both A & B, to get the length of C. All we know at the moment is the x,y coordinates of our two points, so we need to do one more thing first.
By subtracting point one’s X value from point two’s X value, we can get the length of the B side, and the same goes for using the Y values, for finding the A sides length.
You can think of this like so. If x₁ = 1000 and x₂ = 250, the distance between them after subtraction is = 750. Along the x axis, aka side B
So our formula becomes this modified Pythagorean Theorem.
With this we can solve for C, and get our distance value in 2D!
And by expanding it by one more axis, we can also get a value in 3D, with the following formula.
2D Distance In Nuke
Knowing what we do now, let’s create the Pythagorean Theorem with nukes expression language, to find the distance between two 2D points.
Step #1
Create a NoOp node, and add the following knobs to it
2D position knob named “point_one”
2D position knob named “point_two”
Floating Point Slider named “distance”
Step #2
Open the expression editor on the distance knob, and type in the following formula
sqrt((pow2((point_one.x)-(point_two.x)))+(pow2((point_one.y)-(point_two.y))))
This is the modified Pythagorean Theorem we talked about above, but written in Nukes expression language. The sqrt part at the start returns the non-negative square root of everything between the brackets. The pow2 parts are the same thing as writing A^2 (A to the power of 2). And the rest is as described in the original formulas.
Step #3
Now you can move the two point knobs around, and the expression on the distance knob will return the distance between the two
What is this 2D version useful for? I’m not sure, but maybe it can be used to drive some GUI elements, or in very specific situations you could use the distance value to dynamically animate something in screen space. In the next section, we will take a look at the much more useful 3D version.
Bellow is the NoOp node script, if you want to skip the above part, and just see the example
set cut_paste_input [stack 0] version 12.2 v11 push $cut_paste_input NoOp { name Distance_2D selected true xpos -763 ypos 961 addUserKnob {20 User} addUserKnob {12 point_one} point_one {150 250} addUserKnob {12 point_two} point_two {146 252} addUserKnob {7 distance R 0 1000} distance {{sqrt((pow2((point_one.x)-(point_two.x)))+(pow2((point_one.y)-(point_two.y))))}} }
3D Distance In Nuke
Expanding our knowledge a bit more, let’s find the distance between two 3D points, and use that to drive the focal plane on a ZDefocus node
Step #1
Create the following nodes
A Camera named “Cam”
An Axis named “Axis”
A Scene node connecting the Camera and Axis
A ZDefocus
Step #2
Open the expression editor on the ZDefocus focus plane knob (C), and type in the following formula.
sqrt((pow2((parent.Axis.translate.x)-(parent.Cam.translate.x)))+(pow2((parent.Axis.translate.y)-(parent.Cam.translate.y)))+(pow2((parent.Axis.translate.z)-(parent.Cam.translate.z))))
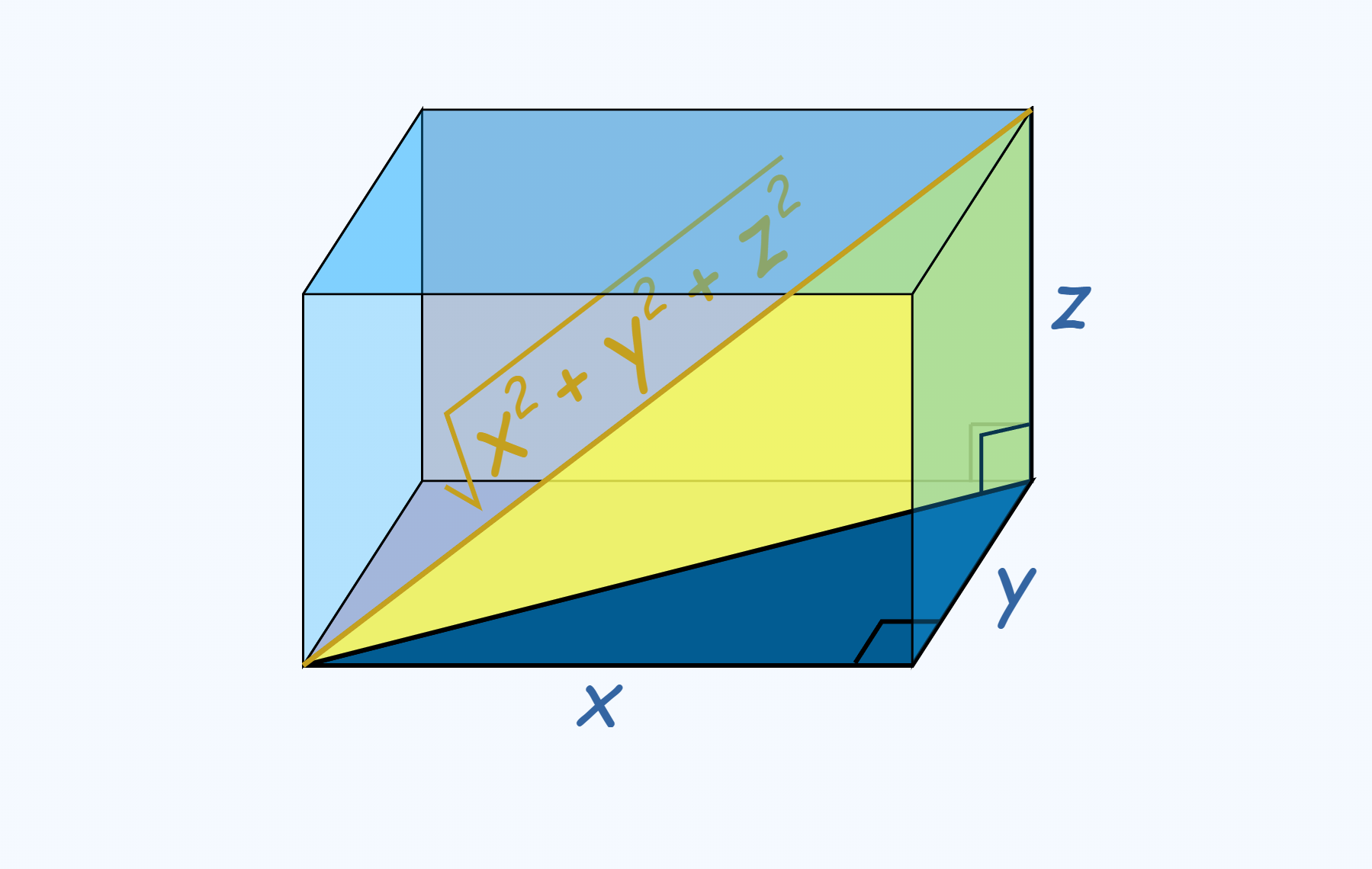
This is the same formula as in the 2D section, but with an extra Z axis. Adding the additional axis is as simple as duplicating either the X or Y sections, and changing it to look for Z values instead.
If you are wondering why this works in 3D so easily, it’s because we are essentially still just making right angle triangles, as show on this brilliant website
Step #3
Now you can move either the Camera or Axis node around, and the expression on the ZDefocus will return the focal plane between the two of them (aka distance)
This 3D version of the formula is much more useful, and can allow you to automatically determine the focal plane throughout a shot. In a pipeline setting, I will often ask that our hero characters have a custom locator placed between their eyes, which can then later been loaded into an Axis node in nuke. Once you have that, you are all set to have everything in focus, all the time!
Bellow is the nuke script, if you want to skip the above part, and just see the example
set cut_paste_input [stack 0] version 12.2 v11 push $cut_paste_input ZDefocus2 { channels rgba math depth center {{sqrt((pow2((parent.Axis.translate.x)-(parent.Cam.translate.x)))+(pow2((parent.Axis.translate.y)-(parent.Cam.translate.y)))+(pow2((parent.Axis.translate.z)-(parent.Cam.translate.z))))}} blur_dof false legacy_resize_mode false show_legacy_resize_mode false name ZDefocus1 selected true xpos 296 ypos -92 } Camera2 { inputs 0 rotate {0 180 0} name Cam selected true xpos 84 ypos -238 } Axis2 { inputs 0 translate {1.5 -43.5 241} name Axis selected true xpos 232 ypos -239 } Scene { inputs 2 name Scene1 selected true xpos 154 ypos -134 }
▽△▽ Praise Pythagoras △▽△